Answer:
1) He originally bought 30 pigs.
2) 30/7 hours
Explanation:
Question 1
Let
 be the number of pigs the farmer bought.
be the number of pigs the farmer bought.
If the farmer paid $210 for
 pigs, then the cost per pig was:
pigs, then the cost per pig was:

If he made $8 of profit per pig sold, then the selling price of each pig was:

If he paid $210 for the pigs and his total profit was $150, then the total income from selling the pigs was:

If 6 pigs died before he could sell the rest, the number of pigs sold was:
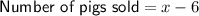
So, the total income from selling the pigs is equal to the number of pigs sold multiplied by the selling price per pig:
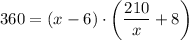
To determine the number of pigs the farmer original bought, solve the equation for x:
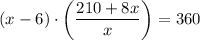
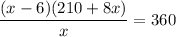
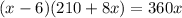
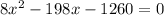
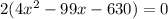
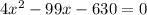
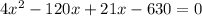

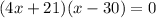
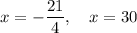
As the number of pigs originally sold cannot be negative, x = 30 is the only valid solution. Therefore, the farmer originally bought 30 pigs.

Question 2
Let K be Kaleb's work rate (the amount of work he can do per hour).
Let T be Trashia's work rate (the amount of work she can do per hour).
Kaleb completes the job in 10 hours, so his work rate is:

Working together, Kaleb and Trashia can complete the job in 3 hours, so their combined work rate is:

To find Trashia's work rate (T), substitute K = 1/10 into the equation for K + T:

Now, solve for T:
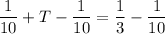
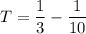
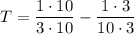
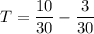
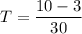
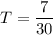
So, Trashia's work rate is 7/30 of the job per hour.
Now, to find how long it would take Trashia to do the job alone, take the reciprocal of her work rate:

Therefore, Trashia would take 30/7 hours to complete the job on her own.