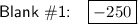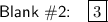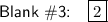Answer:
![-250 \sqrt[3]{2}](https://img.qammunity.org/2024/formulas/mathematics/college/a8r7xsnamwox9qcawjlu58rt6psgu94ink.png)
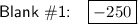
Explanation:
Given expression:
![5\sqrt[3]{5}\cdot \left(-10\sqrt[3]{50}\right)](https://img.qammunity.org/2024/formulas/mathematics/college/nbl7e6m9wu9xycd4f06lyffsgd4dj01mx0.png)
To multiply the given radicals, begin by applying the Commutative Property of Multiplication. This property states that the order in which we multiply numbers does not affect the result.
Collect the coefficients (the numbers outside the radicals) and the radicals:
![5\cdot \left(-10\right) \cdot \sqrt[3]{5}\cdot \sqrt[3]{50}](https://img.qammunity.org/2024/formulas/mathematics/college/27yr76rhrh52jhvoy165qw3uqhn8vey4co.png)
Multiply the coefficients:
![(-50) \cdot \sqrt[3]{5}\cdot \sqrt[3]{50}](https://img.qammunity.org/2024/formulas/mathematics/college/vgif3346kephmqubsyo1e3jlcvj5tubder.png)
![\textsf{Since the indices of the radicals are the same, we can apply}\\\\\textsf{the radical rule}\;\;\sqrt[n]{\vphantom{b}a}\sqrt[n]{b}=\sqrt[n]{ab}\;:](https://img.qammunity.org/2024/formulas/mathematics/college/fmjjnbbuxvf76mz4zxed57a2pj9ea64yza.png)
![(-50) \cdot \sqrt[3]{5\cdot50}](https://img.qammunity.org/2024/formulas/mathematics/college/z6u99z2xgkm90cjj7j5n1kryhi20twf3an.png)
![(-50) \cdot \sqrt[3]{250}](https://img.qammunity.org/2024/formulas/mathematics/college/wszhhgkdkqf6eovo22tks6fwq6v58kc48r.png)
Rewrite 250 as the product of 125 and 2:
![(-50) \cdot \sqrt[3]{125 \cdot 2}](https://img.qammunity.org/2024/formulas/mathematics/college/2afp5ynzmlx9pad9v7jhj25kqqze7xwmrb.png)
As 5³ = 125, then:
![(-50) \cdot \sqrt[3]{5^3 \cdot 2}](https://img.qammunity.org/2024/formulas/mathematics/college/sj6lz4cek2zclv8pkprg0idll8w26mar7b.png)
![\textsf{Apply the radical rule:} \quad \sqrt[n]{ab}=\sqrt[n]{\vphantom{b}a}\sqrt[n]{b}](https://img.qammunity.org/2024/formulas/mathematics/college/5e9gbx22455ako29qhr9x44ooo6slwutag.png)
![(-50) \cdot \sqrt[3]{5^3}\cdot \sqrt[3]{2}](https://img.qammunity.org/2024/formulas/mathematics/college/fpr806ia0onmuvnboazbqgrgxxh6ugam3s.png)
![\textsf{Apply the exponent rule:} \quad \sqrt[n]{a^m}=a^{(m)/(n)}](https://img.qammunity.org/2024/formulas/mathematics/high-school/yyxhplirudk19gm0gby206z212tuqiy4eh.png)
![(-50) \cdot 5^{(3)/(3)}\cdot \sqrt[3]{2}](https://img.qammunity.org/2024/formulas/mathematics/college/mfhnnsopjkqt2tbgkqb2z1fe78il1dq4li.png)
![(-50) \cdot 5^(1)\cdot \sqrt[3]{2}](https://img.qammunity.org/2024/formulas/mathematics/college/d7dn2qrx7eupcr0om37d0y3l3pk3o7zj8s.png)
![(-50) \cdot 5\cdot \sqrt[3]{2}](https://img.qammunity.org/2024/formulas/mathematics/college/or1kx11nopbh8s3q2h7par4k7vlnpht7p3.png)
Multiply -50 and 5:
![-250 \cdot \sqrt[3]{2}](https://img.qammunity.org/2024/formulas/mathematics/college/bkh9a9vodxnu0mfy7ucl7kj3lcvd7cidl6.png)
Therefore, the product of the radicals in its simplest form is:
![\Large\boxed{\boxed{-250 \sqrt[3]{2}}}](https://img.qammunity.org/2024/formulas/mathematics/college/ilmr6r313lxq481kgmhyx64rv80r65awuj.png)
The answer in terms of the blanks in order from left to right is: