Answer:

Step-by-step explanation:
Hello!
In this case, since we have hot and cold water, we infer that as hot water cools down, cool water heats up based on the first law of thermodynamics; thus, we can write:

In such a way, we can write the expression in terms of mass, specific heat and temperature change:
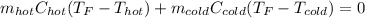
However, since they both have the same specific heat and the same mL are in g due to the 1.00-g/mL density, we obtain:
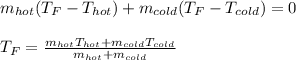
Now, we plug in to obtain:
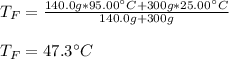
Best regards!