Question

Need answer quick pllss​

Answer 1

a) 9.8 metres per second

b) 11.2 metres per second

c) 2.2 meters per second squared

Explanation:

The provided velocity-time graph shows that the runner accelerated from rest for the first 5 seconds of the race, then ran at a constant speed until he finished the race at 20.32 seconds. The total distance of the race was 200 meters.

a) Average Speed

The average speed can be calculated by dividing the total distance traveled by the total time taken. In this case, the total distance was 200 meters, and the total time was 20.32 seconds, so:

`\sf \textsf{Average speed}=(200\; m)/(20.32\;s)=9.8\; m/s`

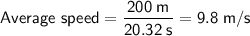
Therefore, the runner's average speed was 9.8 metres per second (rounded to one decimal place).

b) Maximum Speed

To find the maximum speed, we need to identify the highest point on the velocity-time graph. In this case, it is the part of the graph where the runner ran at a constant speed. Let the maximum speed be v.

In a velocity-time graph, the area under the graph represents the total distance traveled. Therefore, to determine the maximum speed (v), we can create an equation by summing the areas of the triangle and rectangle (both with a height of v) and equating it to the total distance traveled (200 meters):

`(1)/(2) \cdot 5 \cdot v + (20.32-5) \cdot v=200`

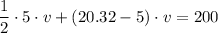
Solve the equation for v:

`\begin{aligned}(1)/(2) \cdot 5 \cdot v + (20.32-5) \cdot v&=200\\\\2.5v + 15.32v&=200\\\\17.82v&=200\\\\v&=(200)/(17.82)\\\\v&=11.2\; \sf m/s\;(1\;d.p.)\end{aligned}`

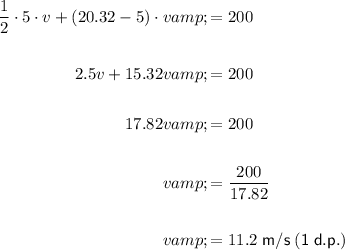
Therefore, the runner's maximum speed was 11.2 metres per second (rounded to one decimal place).

c) Acceleration

A sloping line on a velocity-time graph shows that the object is accelerating. The slope of the line is equal to the acceleration. Therefore, the formula for acceleration is:

`\sf Acceleration = \frac{\textsf{Change in velocity}}{\textsf{Change in time}}=(\Delta v)/(\Delta t)`

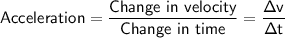
From the graph, we see that the runner started from rest (0 m/s) and reached a constant velocity of approximately 11.2 m/s after 5 seconds. Therefore:

`\sf Acceleration = (11.2-0)/(5-0)=(11.2)/(5)=2.2\; m/s^2`

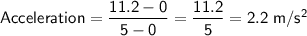
So, the acceleration over the first 5 seconds was approximately 2.2 meters per second squared (rounded to two significant figures).