Answer:
Hi,
Explanation:
To find the percentage of students who would be expected to score between 74 and 78 on Mr. Emmer's Chemistry test, you can use the z-score and the standard normal distribution (also known as the Z-distribution).
First, you need to find the z-scores for both 74 and 78 using the given mean (μ=82) and standard deviation (σ=4):
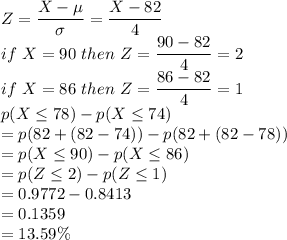
Now, you want to find the percentage of students who score between -2 and -1 on the standard normal distribution curve. You can do this using a standard normal distribution table or a calculator.
The area between -2 and -1 on the standard normal distribution curve represents the percentage of students in this range.
You can find this using a standard normal distribution table or a calculator. It's typically about 0.1359, which means approximately 13.59% of students would be expected to score between 74 and 78 on Mr. Emmer's Chemistry test.