Question

Ivanna bought a desktop computer and a laptop computer. Before finance charges, the laptop cost $450 less than the desktop. She paid for the computers using two different financing plans. For the desktop the interest rate was 6.5% per year, and for the laptop it was 9% per year. The total finance charges for one year were $409. How much did each computer cost before finance charges?

Answer 1

desktop price be x
laptop price (x+450)
For the desktop the interest rate was 9% per year,
Interest = 9%x
and for the laptop it was 6% per year.
Interest = 6%(x+450)
The total finance charges for one year were $300

9%x + 6%(x+450) = 300
9x+6(x+450) = 300*100
9x+6x +2700=30000
15x= 30000-2700
15x=27300
x= 1820

Answer 2

According to the problem, the laptop costs $450 less than the desktop. Let x the cost of the laptop, then we get the following equation:

`x\text{ + 450 = cost of the desktop}`

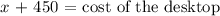
now, the total finance charge of $409 is from 9% of the cost of the laptop and 6.5% of the cost of the desktop. According to this, we get the following equation:

`0.09(x)+0.065(x+450)=409`

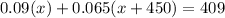
Applying the distributive property, we get:

`0.09x+0.065x+29.25=409`

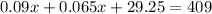
now, placing like terms on each side of the equation, we get:

`0.09x+0.065x=409-29.25`

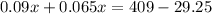
this is equivalent to:

`0.155x\text{ = 379.75}`

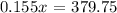
solving for x, we get:

`x\text{ = }(379.75)/(0.155)=2450`

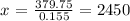
this means that:

The cost of the laptop is x = 2450

and

The cost of the desktop is x+450 = 2450 +450 = 2900.

So that, we can conclude that the correct answer is:

Cost of the laptop = 2450

Cost of the desktop =2900.