Question

Hi I need help with this i’m in a hurry so can you please just tell me the answer lol sorry i’m just in a little rush

Answer 1

Step 1

In the example why is the area of one triangle multiplied by 2.

This is because the hexagon is divided into one rectangle and 2 congruent triangles. Therefore, the area of the two triangles will be the same since they are congruent triangles. In order to get the area of the hexagon, the area of one of the triangles is mutiplied by 2 and added to the area of the rectangle.

Step 2

Find the dimension of one of the shaded triangle from Bev's pattern.

`\begin{gathered} \\ \text{For Bev's triangle;} \\ \text{base}=4 \\ \text{height}=3 \\ Slantheight^2=(\text{ }(base)/(2))^2+height^2 \\ Slantheight^2=((4)/(2))^2+3^2 \\ Slantheight^{}=\sqrt[]{2^2+9} \\ Slantheight=\sqrt[]{13}\text{unit} \end{gathered}`

The dimensions will therefore be;

`\begin{gathered} \text{base= 4unit} \\ \text{slant height=}\sqrt[]{13}unit \\ \text{slant height=}\sqrt[]{13}unit \end{gathered}`

What can you say about the shaded area of all the shaded triangles in Bev's pattern.

`\begin{gathered} \text{Area of given triangle=6unit}^2 \\ \text{Area of Bev's triangle=}(1)/(2)*4*3=6unit^2 \end{gathered}`

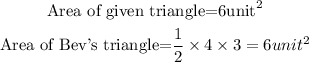
The area of all shaded triangles in Bev's pattern are equal. This is because all the shaded triangles have the same dimensions and can be said to be congruent. Hence, they will have the same area.