Answer
The inverse function is
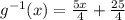
The domain of this inverse function is all real numbers.
Step-by-step explanation
The question asks us to find the invers of the given function and give any restrictions of the domain if that exists.
The function is
g(x) = -5 + (4x/5)
To obtain the inverse of a function, the right approach is to write g(x) as y, then make x the subject of formula.
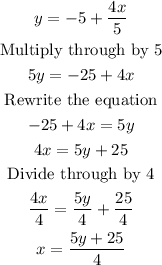
We can then write this properly in terms of the inverse function
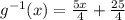
The domain of a function refers to the values of the independent variable (x), where the dependent variable [y or f(x)] or the function has a corresponding real value. The domain is simply the values of x for which the output also exists.
The domain of this inverse function is all real numbers because there would be a real number answer for every real number value of x.
Hope this Helps!!!