Question

Y = -4x+6
3x + 4y = -2

is (2,2) a solution of the system?

Answer 1

No

Explanation:

(2,-2)can be a solution but (2,2) can't

Answer 2

No, (2,2) is not a solution of the system.

Solution is (2-2)

Explanation:

To solve the system of equations y = - 4x + 6 and 3x + 4y = -2, we can use the substitution method.

First, we need to solve one of the equations for one of the variables. In this case, we can solve the first equation for y:

y = -4x+6

Now, we can substitute this expression for y in the second equation:

3x + 4(-4x+6) = -2

Distribute the parenthesis.

3x - 16x + 24 = -2

We can now combine like terms and solve for x:

-13x + 24 = -2

Subtract 24 on both sides.

-13x + 24 - 24= -2 - 24

-13x = -26

Divide both sides by -13.

`\sf (-13x)/(13)=(-26)/(-13)`

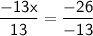
x = 2

Now that we know that x = 2, we can substitute this value for x in either of the original equations to solve for y. We will use the first equation:

y = -4 (2)+6

y = -8+6

y = -2

Therefore, the solution to the system of equations y = -4x+6 and 3x + 4y = -2 is (2, -2).

So,

(2,2) is not a solution of the system.