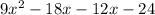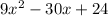Question

(3x-4)(3x-6) as a trinomial

Answer 1

To find the product of (3x-4)(3x-6) as a trinomial, we use the distributive property to multiply each term and then combine like terms.

Step-by-step explanation:

To find the product of (3x-4)(3x-6) as a trinomial, we can use the distributive property. We multiply each term of the first binomial by each term of the second binomial, and then combine like terms. Here's how:

(3x)(3x) + (3x)(-6) + (-4)(3x) + (-4)(-6)

9x^2 - 18x - 12x + 24

Combining like terms, we have: 9x^2 - 30x + 24

Answer 2

The trinomial we get when expanding the binomials is
`9x^2-30x+24`.

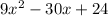To answer this question we can use the FOIL method expanding binomials.

FOIL Method:

• used for distributing binomials
• F - First
• O - Outer
• I - Inner
• L - Last

(3x-4)(3x-6)

F - We can multiply 3x (first) by the 3x (first) in the second binomial.

`3x* 3x = 9x^2`

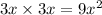
O - We can multiply 3x by the outer one in the second binomial, -6.

`3x* -6=-18x`

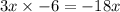
I - We can multiply the inner of the first bracket to the inner of the second bracket, -4 and -6 respectively.

`-4* 3x=-12x`

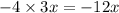
L - We can multiply the second term in the first bracket by the last term in the second bracket.

`-4*-6=24`

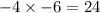
Then we can combine like terms to convert it to trinomial form.

`9x^2-18x-12x-24`

`9x^2-30x+24`