Answer:
A
Explanation:
We are given:
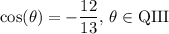
Since cosine is the ratio of the adjacent side over the hypotenuse, this means that the opposite side is (we can ignore negatives for now):
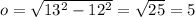
So, the opposite side is 5, the adjacent side is 12, and the hypotenuse is 13.
And since θ is in QIII, sine/cosecant is negative, cosine/secant is negative, and tangent/cotangent is positive.
Cosecant is given by the hypotenuse over the opposite side. Thus:
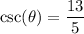
Since θ is in QIII, cosecant must be negative:

Our answer is A.