Question

Simplify (7 + 2√50)(5 - 2√2)

Give your answer in the form a + b√18

Where:
a and b are integers.

Answer 1

`\sf -5 + 12√( 18)`

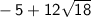
Explanation:

To Simplify:

`\sf \left(7 + 2√(50)\right)\left(5 - 2√(2)\right)`

Solution:

To simplify the expression, we can use the distributive property.

`\sf = 7\left(5 - 2√(2)\right) + 2√(50)\left(5 - 2√(2)\right)`

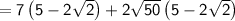
Simplifying each term by opening parenthesis, we get:

`\sf = 7\cdot 5 - 7\cdot 2√(2) + 2√(50)\cdot 5 - 2√(50)\cdot 2√(2)`

`= 35 - 14√(2) + 10√(50) - 4 √(100)`

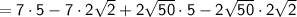
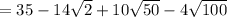
Simplifying the term
`\sf √(100)`, we get:

`\sf = 35 - 14√(2) + 10√(50) - 4 √(10^2)`

`\sf = 35 - 14√(2) + 10√(50) - 4\cdot 10`

`\sf = 35 - 14√(2) + 10√(50) - 40`

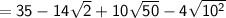
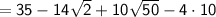
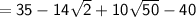
Combining the remaining terms, we get:

`\sf = 35 - 40 - 14√(2) + 10√(50)`

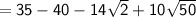
We have simplified
`\sf 5√(50)` further by factoring
`\sf √(50)` as
`\sf √(5^2 \cdot 2)`

`\sf = -5 - 14√(2) + 10√(5^2\cdot 2 )`

`\sf = -5 - 14√(2) + 10\cdot 5 √(2)`

`\sf = -5 - 14√(2) + 50√(2)`

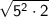
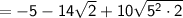
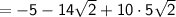
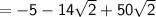
Simplify like terms:

`\sf = -5 + 36√(2)`

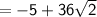
We express
`√(2)` as
`\sf √(18)` by multiplying 9 inside the square root and dividing by 3 in outside as
`√(9)=3`

`\sf = -5 + (36)/(3)√(9 \cdot 2 )`

`\sf = -5 + 12√( 18)`

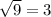
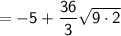
Therefore, answer in the form
`\sf a + b√( 18)` is:

`\sf -5 + 12√( 18)`

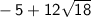
Where, while comparing, we get

• a = -5
• b = 12

Note:

The distributive property is a mathematical property that states that multiplication distributes over addition and subtraction.

This means that we can multiply a number by a sum or difference of two or more numbers by multiplying each number in the sum or difference individually by the number and then adding or subtracting the products.

The distributive property can be expressed in the following formula:

`\boxed{\boxed{\sf a(b + c) = ab + ac}}`

where a, b, and c are any numbers.