Question

A tract of land, indicated by Quadrilateral MNPQ, is shown on this grid where one square unit represents 50 square feet.What is the area, in square feet, of the tract of land?

Answer 1

We have to find the area of the quadrilateral MNPQ.

We can divide it in two right triangles and then calculate the area as the sum of the area of the two triangles. To do that we would have to calculate the distances between N and P and M and N, as this are the legs of the upper triangle.

We can simplify it by making three right triangles by adding one vertex R(1,0):

Now, the length of the legs of the triangles are easier to find.

We then can calculate the area of the quadrilateral (A) as:

`\begin{gathered} A=A_{\text{MRN}}+A_{\text{PRN}}+A_{\text{MPQ}} \\ A=((MR)\cdot(RN))/(2)+((PR)\cdot(RN))/(2)+((MP)(PQ))/(2) \\ A=(1)/(2)(9\cdot6+4\cdot6+13\cdot8) \\ A=(1)/(2)(54+24+104) \\ A=(1)/(2)\cdot182 \\ A=91 \end{gathered}`

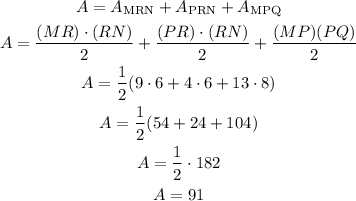
The area covers 91 square units.

As each unit represents 50 square feet, we can calculate the area in feet as:

`A=91\text{ sq. units}\cdot\frac{50\text{ sq. ft.}}{1\text{ sq. unit}}=4550\text{ sq. ft.}`

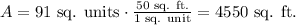
Answer: the land's area is 4550 square feet.