Question

Two charges are placed as shown in the figure. The distance

between charges is 13.0 cm. Point P is 5.0 cm from the charge
91 and 12.0 cm from the charge q2. The magnitude of q₁ is
3.00 μC, but its sign and the value of the charge q2 are not
known. The direction of the net electric field E at point Pis entirely
in the negative y-direction. (Figure 1)

Answer 1

Both
`q_(1)` and
`q_(2)` should be negative.

The net electric field at
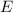`E` would be approximately
`1.16 * 10^(4)\; {\rm N\cdot C^(-1)}`.

Step-by-step explanation:

The
`x\!\!`-components of the fields from
`q_(1)\!` and
`q_(2)\!` to point in opposite directions to balance each other.

Because
`\!q_(1)` and
`\!q_(2)` are on opposite sides of
`P`, these two charges need to either simultaneously attract or repel any test charge placed at
`P\!`. Therefore, the sign of
`q_(1)\!` and
`q_(2)\!` need to be the same.

In this question, because
`q_(1)\!` and
`q_(2)\!` have the same sign, the
`y`-component of the electric field at
`P` from
`q_(1)` and
`q_(2)` would point in the same direction. Because this direction points towards the two charges (downward, not upward),
`q_(1)` and
`q_(2)` both should be negative.

The net electric field at point
`P` can be found in the following steps:

• Find the magnitude of the electric field at point
  `P` from charge
  `q_(1)`.
• Find the
  `x`-component and
  `y`-component of the electric field at point
  `P` from
  `q_(1)`.
• Thus, the
  `x\!`-component of the field from
  `q_(2)\!` should be equal in magnitude to
  `\!x`-component of the field from
  `q_(1)\!`.
• Find the
  `y`-component of the electric field at point
  `P` from
  `q_(2)` from the
  `x`-component of this field.
• Take the sum of the
  `y`-component of the electric field at
  `P` from
  `q_(1)` and from
  `q_(2)` to obtain the net electric field at that position.

Apply Coulomb's Law to find the magnitude of the electric field at
`P` from
`q_(1)`:

`\displaystyle E_(1) = \frac{k\, q}{{r_(1)}^(2)}`,

Where:

• 
  `q_(1) = 3.00\; {\rm \mu C} = 3.00 * 10^(-9)\; {\rm C}`,
• 
  `k \approx 8.9876 * 10^(8)\; {\rm N\cdot m^(2)\cdot C^(-2)}` is Coulomb's constant, and
• 
  `r_(1) = 5.0\; {\rm cm} = 5.0 * 10^(-2)\; {\rm m}` is the distance between
  `q_(1)` and point
  `P`.

Note that for consistency, all quantities should be measured in standard units.

The electric field at
`P` from
`q_(1)`, the
`x`-component of this field, and the
`y`-component of this field form a right triangle. This right triangle is similar to the right triangle connecting
`P\!`,
`q_(1)\!`, and
`q_(2)\!`. The ratio between the magnitude of this field, magnitude of the
`x`-component of this field, and magnitude of the
`y`-component of this field would be
`13.0: 5.0 : 12.0`.

Let
`E_(1)` denote the magnitude of this field at point
`P`. Magnitude of the
`x`-component would be
`(5/13)\, E_(1)`. Magnitude of the
`y`-component would be
`(12/13)\, E_(1)`.

At point
`P`, the
`x`-component of the field from
`q_(1)` and
`q_(2)` are balanced. Hence, the magnitude of the
`x\!`-component of the field from
`q_(2)\!` would be equal to the
`\!x` component of the field from
`q_(1)`, which is equal to
`(5/13)\, E_(1)`.

Similar to the electric field at point
`P` from
`q_(1)`, the electric field from
`q_(2)` would also form a right triangle with the
`x`-component and
`y`-component of this field. However, unlike the field from
`\!q_(1)`, the ratio between the magnitude of this field, magnitude of the
`x\!`-component, and magnitude of the
`y\!`-component would be
`13.0 : 12.0 : 5.0`. Specifically, the ratio between the magnitude of the
`\!x`-component and that of the
`\!y`-component would be
`12.0 : 5.0`.

Since the magnitude of the
`x`-component of the field at point
`P` from
`q_(2)` is
`(5/13)\, E_(1)`, the magnitude of the
`y`-component of this field would be:

`\displaystyle (5)/(12)\, \left((5)/(13)\, E_(1)\right)`.

The net electric field at point
`P` is equal to the sum of the
`y`-component of the field from
`q_(1)` and the
`y\!`-component of the field from
`q_(2)`:

`\begin{aligned} & (12)/(13)\, E_(1) + (5)/(12)\, \left((5)/(13)\, E_(1)\right)\\ =\; & \left((12)/(13) + \left((5)/(12)\right)\, \left((5)/(13)\right)\right)\, \left(\frac{k\, q_(1)}{{r_(1)}^(2)}\right) \\ \approx\; & 1.16 * 10^(4)\; {\rm N\cdot C^(-1)} \end{aligned}`.

In other words, the net electric field at point
`P` would.be approximately
`1.16* 10^(4)\; {\rm N\cdot C^(-1)}` (in the negative
`y`-direction.)