Question

Writing Quadratic Equations

Answer 1

Explanation:

Given:

• vertex (p, q) = (3, 9)
• roots (x₁, 0) & (x₂, 0) = (0, 0) & (6, 0)

`\boxed{vertex\ form: f(x)=a(x-p)^2+q}`

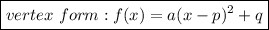
f(x) = a(x-3)² + 9

[in order to find value of a, substitute x & f(x) with any coordinate from the parabola, e.g.(0, 0)]

0 = a(0-3)² + 9

0 = 9a + 9

a = -1

Therefore:

vertex form : f(x) = -(x-3)² + 9

To find the standard form, just expand the vertex form:

f(x) = -(x-3)² + 9

f(x) = -(x²-6x+9) + 9

f(x) = -x² + 6x

To find the intercept form, just factorize the standard form

f(x) = -x² + 6x

f(x) = -(x² - 6x)

f(x) = -x(x - 6)