Question

(need asap, worth 100 points)The graph of a function defined for x ≥ 0 is given. Complete the graph for x < 0 to make a) an even

function and b) an odd function.

Answer 1

See the attached graphs.

Explanation:

Part a: Even function

The graph of an even function is symmetric with respect to the y-axis. This means that if we draw one-half of the graph (usually the right half), we can simply reflect it across the y-axis to obtain the other half.

Mathematically, a function f(x) is even if it satisfies the following property for all values of x in its domain:

`\large\boxed{(x,y)=(-x,y)}`

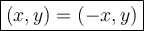
So, if we have a point (a, b) on the known side, reflect it to (-a, b) on the other side. This essentially means negating the x-coordinate while keeping the y-coordinate unchanged.

The right side of the graph is a straight line from the origin (0, 0) to point (5, -6). Therefore, the left side of the graph is a straight line from the origin (0, 0) to point (-5, -6).

`\hrulefill`

Part b: Odd function

The graph of an odd function is symmetric with respect to the origin (0, 0). This means that if we draw one-half of the graph, we can mirror it across the origin to obtain the other half.

Mathematically, a function f(x) is odd if it satisfies the following property for all values of x in its domain:

`\large\boxed{(x,y)=(-x,-y)}`

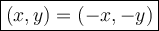
So, if we have a point (a, b) on the known side, reflect it to (-a, -b) on the other side. This essentially means negating both the x-coordinate and the y-coordinate.

The right side of the graph is a straight line from the origin (0, 0) to point (5, -6). Therefore, to make it an odd function, draw a straight line from (0, 0) to (-5, 6).