Question

The monthly cost (in dollars) of a long-distance phone plan is a linear function of the total calling time (in minutes). The monthly cost for 37 minutes of calls is$13.21 and the monthly cost for 70 minutes is $17.50. What is the monthly cost for 45 minutes of calls?

Answer 1

Given:

The monthly cost is 37 min is $13.21

70 min cost is $17.50

Find-:

The monthly cost for 45 minutes of calls

Explanation-:

The linear equation is:

`\begin{gathered} y=mx+c \\ \end{gathered}`

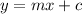
Where,

`\begin{gathered} m=\text{ Slope} \\ \\ c=Y-\text{ Intercept} \end{gathered}`

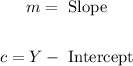
The formula of the slope is:

`m=(y_2-y_1)/(x_2-x_1)`

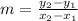
The point is:

`\begin{gathered} (x_1,y_1)=(37,13.21) \\ \\ (x_2,y_2)=(70,17.50) \end{gathered}`

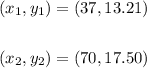
So, the slope is:

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ \\ m=(17.50-13.21)/(70-37) \\ \\ m=(4.29)/(33) \\ \\ m=0.13 \end{gathered}`

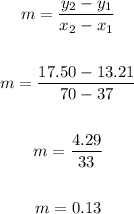
Slope is:

The general equation of a line:

`\begin{gathered} y=mx+c \\ \\ y=0.13x+c \end{gathered}`

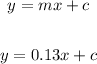
The value of "c" is:

`\begin{gathered} y=0.13x+c \\ \\ (x,y)=(37,13.21) \\ \\ 13.21=0.13(37)+c \\ \\ c=13.21-4.81 \\ \\ c=8.4 \end{gathered}`

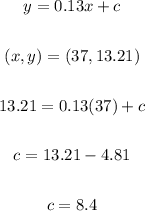
The equation is:

`\begin{gathered} y=mx+c \\ \\ y=0.13x+8.4 \end{gathered}`

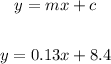
Cost at 45 min. is:

`\begin{gathered} x=45 \\ \\ y=0.13x+8.4 \\ \\ y=0.13(45)+8.4 \\ \\ y=5.85+8.4 \\ \\ y=14.25 \end{gathered}`

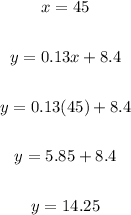
The 45 min cost is $14.25