Question

Dustin boat traveled 36 miles downstream in three hours. The same boat traveled 30 miles upstream in five hours. What is the speed of the boat and the speed of the current

Answer 1

The speed of the boat is 9 miles/hour and the speed of the current is 3 miles/hour

Step-by-step explanation:

Let's call x the speed of the boat and y the speed of the current.

The distance traveled is equal to the speed times the time, so the boat traveled 36 miles in three hours and we can write the following equation

(x + y)3 = 36

3(x + y) = 36

because when the boat traveled downstream, the total speed is the sum of x and y.

On the other hand, the boat traveled 30 miles upstream in 5 hours, so

(x - y)5 = 30

5(x - y) = 30

Therefore, the system of equations is

3(x + y) = 36

5(x - y) = 30

Solving the first equation for x, we get

`\begin{gathered} 3(x+y)=36 \\ \\ (3(x+y))/(3)=(36)/(3) \\ \\ x+y=12 \\ x+y-y=12-y \\ x=12-y \end{gathered}`

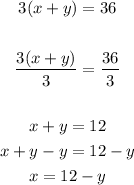
Now, we can replace this expression on the second equation as follows

`\begin{gathered} 5(x-y)=30 \\ \\ {(5(x-y))/(5)}=(30)/(5) \\ \\ x-y=6 \\ \\ \text{ Replacing x = 12 - y} \\ 12-y-y=6 \\ 12-2y=6 \\ 12-2y-12=6-12 \\ -2y=-6 \\ \\ (-2y)/(-2)=(-6)/(-2) \\ \\ y=3 \end{gathered}`

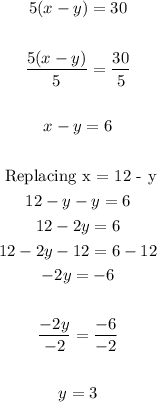
Then, the value of x is

x = 12 - y

x = 12 - 3

x = 9

So, the speed of the boat is 9 miles/hour and the speed of the current is 3 miles/hour