Question

The student council members at Silver City Middle School are planning the school's carnival. They are considering renting coin-operated games for students to play. The cost to rent each coin-operated game is $100. The budget will allow them to rent up to 5 of the games. The function C(g) represents how much it'll cost the student council, in dollars, to rent g coin-operated games.

What is the range of C(g)?

Answer 1

The range of C(g) is $500.

To calculate this, we know that the cost of renting one coin-operated game is $100, so the cost of renting five games would be:

C(g) = 5 x $100 = $500

Therefore, the range of C(g) is $500.

Explanation:

Answer 2

Range: {0, 100, 200, 300, 400, 500}

Explanation:

The range of C(g) is the set of all possible values that C(g) can take.

The minimum value of C(g) is $0, which occurs when g = 0 (i.e., they rent no games).

The maximum value of C(g) is $500, which occurs when g = 5 (i.e., they rent the maximum number of games). Therefore, the range of C(g) is:

{0, 100, 200, 300, 400, 500}

Another way to solve this problem is to use the following formula:

Range of C(g) = Maximum value of C(g) - Minimum value of C(g)

In this case, the maximum value of C(g) is $500 and the minimum value of C(g) is 0, so the range of C(g) is:

`\textsf{Range of C(g) }= \$500 - \$0 = \$500`

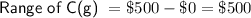
Therefore, the range of C(g) is the set of all possible values that C(g) can take, which is:

{0, 100, 200, 300, 400, 500}