Question

Sue the diagram below to answer the questions on the right: D E 4x° 21 2y+5 2xº F 14 Find the value of y: (a) (b) Solve for x: (c) Find the measure of ZF? (d) What is the measure of ZD?​

Answer 1

a. The value of y is

b. The value of x is
`18^\circ`.

c. The measure of angle F is
`36^\circ`

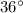
d. The measure of angle D is
`72^\circ`

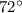
In an isosceles triangle, the angle sum property states that the sum of the three interior angles is always 180 degrees. In this case, you have an isosceles triangle DEF with angles D and E being equal (both 4x) and angle F being 2x.

So, the sum of the angles D, E, and F is 180 degrees:

`\(4x + 4x + 2x = 180^\circ\)`

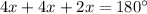
Combine like terms:

`\(10x = 180^\circ\)`

Now, solve for x:

`\[x = (180^\circ)/(10) = 18^\circ\]`

Now that you have the value of x, you can find each angle:

- Angle D and Angle E are both
`\(4x = 4 * 18^\circ = 72^\circ\)`.

- Angle F is
`\(2x = 2 * 18^\circ = 36^\circ\)`.

So, in triangle DEF:

- Angle D = 72 degrees

- Angle E = 72 degrees

- Angle F = 36 degrees.

Since triangle DEF is an isosceles triangle, the sides opposite the equal angles are also equal. Therefore, DF = EF.

Given that DF = 21 and EF = 2y + 5, set them equal to each other:

`\[21 = 2y + 5\]`

Now, solve for y:

`\[2y = 21 - 5\]`

`\[2y = 16\]`

`\[y = 8\]`

So, the value of y is 8.

Answer 2

36°

Explanation:

Triangle is isosceles and angle D is equal to angle E => 180°=4x+4x+2x

10x=180°

x=18°

Angle D is equal 2×18=36°