Answer:
- x = 17
- m∠JKL = 87°
- m∠KJL = 58°
- m∠KLJ = 35°
- m∠KLM = 145°
Explanation:
Since exterior angle of a triangle is equal to the sum of two interior opposite angles.
So,
m∠JKL + m∠KJL = m∠KLM
Substitute the given value:
(7x - 32)° + (5x -27)° = (9x - 8)°
7x -32 +5x -27 = 9x - 8
Simplify like terms:
12x - 59 = 9x - 8
Add 59 on both sides:
12x - 59 + 59 = 9x - 8 + 59
12x = 9x + 51
Subtract 9x on both sides:
12x - 9x = 9x + 51 - 9x
3x = 51
Divide both sides by 3.
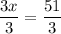
x = 17
Now
We can find the other angles by substitution value of x.
m∠JKL = (7×17 -32)° = (119 - 32)° = 87°
m∠KJL = (5 × 17 - 27)° = (85 - 27)° = 58°
m∠KLM = (9 × 17 - 8)° = (153 - 8)° = 145°
And Finally:
m∠KLJ and m∠KLM are linear pair and they are supplementary means added up to 180°
So,
m∠KLJ + m∠KLM = 180°
Substitute the known value:
m∠KLJ + 145° = 180°
Subtract 145° on both sides:
m∠KLJ + 145° - 145° = 180° - 145°
m∠KLJ = 35°
Summary:
- x = 17
- m∠JKL = 87°
- m∠KJL = 58°
- m∠KLJ = 35°
- m∠KLM = 145°