Answer:
See Below.
Explanation:
The sum of an A.P. is given by:
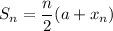
Where n is the number of terms, a is the initial term, and xₙ is the last term.
Therefore:
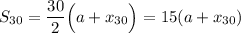
And likewise:
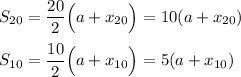
Substitute:
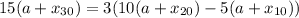
Distribute:

Simplify:
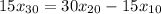
Simplify:
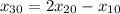
The nth term for an A.P. is:
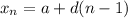
Where a is the initial term and d is the common difference.
So, it follows that:
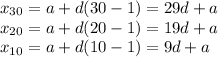
Therefore:
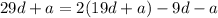
Which follows that:
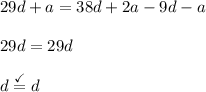
QED.