Answer:
Explanation:
Vertically opposite angles are two angles that are opposite each other when two lines intersect. They are also called vertical angles.
Vertically opposite angles are always equal in measure.
In this case:
(x + 16)° and (4x - 5)° are vertically opposite angles.
So,
(x + 16)° = (4x - 5)°
x + 16 = 4x - 5
Subtract x on both sides.
x + 16 - x = 4x - 5 - x
16 = 3x - 5
Add 5 on both sides:
16 + 5 = 3x - 5 + 5
21 = 3x
Divide both sides by 3.
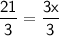
7 = x.
Therefore,
Value of x is 7.
And
(x + 16)° and A are angles of linear pair. And Linear pair angles are supplementary means added up to 180°.
So,
(x + 16)° + A = 180°
Substitute the value of x.
(7 + 16)° + A = 180°
23° + A = 180°
Subtract 23° on both sides.
23° + A - 23° = 180° - 23°
A = 157°
Therefore, the measure of angle A is 157°.