Question

It is a Algebra problemSuppose an object is thrown upward with an initial velocity of 48 feet per second from a height of 120 feet. The height of the object t seconds after it is thrown is given by h(t)=-16t²+48t+120. Find the average velocity in the first two seconds after the object is thrown.

Answer 1

Average velocity in the first 2 seconds = 16 ft/s

Step-by-step explanation

The average value of a function over an interval [a, b] is given as

`\text{Average value of the function = }(1)/(b-a)\int ^b_af(x)dx`

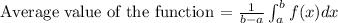
The integral is evaluated over the same interval [a, b]

Since we are asked to find the average velocity over the first 2 seconds, we need to first obtain the funcion for th object's velocity.

Velocity = (dh/dt)

h(t)= -16t² + 48t + 120

Velocity = (dh/dt) = -32t + 48

So, we can then find the average velocity over the first 2 seconds, that is, [0, 2]

`\begin{gathered} \text{Average value of the function = }(1)/(b-a)\int ^b_af(t)dt \\ a=0,b=2,f(t)=-32t+48 \\ \text{Average Velocity = }(1)/(2-0)\int ^2_0(-32t+48)dt \\ =(1)/(2)\lbrack-16t^2+48t\rbrack^{2_{}}_0 \\ =(1)/(2)\lbrack-16(2^2)+48(2)\rbrack_{} \\ =0.5\lbrack-16(4)+96\rbrack \\ =0.5\lbrack-64+96\rbrack \\ =0.5\lbrack32\rbrack \\ =16\text{ ft/s} \end{gathered}`

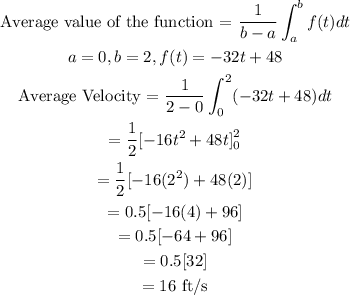
Hope this Helps!!!