Answer
Average velocity in the first 2 seconds = 16 ft/s
Step-by-step explanation
The average value of a function over an interval [a, b] is given as
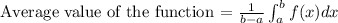
The integral is evaluated over the same interval [a, b]
Since we are asked to find the average velocity over the first 2 seconds, we need to first obtain the funcion for th object's velocity.
Velocity = (dh/dt)
h(t)= -16t² + 48t + 120
Velocity = (dh/dt) = -32t + 48
So, we can then find the average velocity over the first 2 seconds, that is, [0, 2]
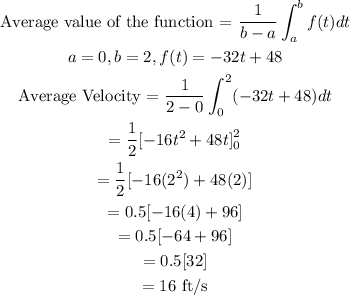
Hope this Helps!!!