Question

Consider the equation 14 x 10^0.5w= 100.Solve the equation for w. Express the solution as a logarithm in base-10.W = _____ Approximate the value of w. Round your answer to the nearest thousandth.w ≈ _____

Answer 1

The logarithmic expression is
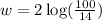`w =2 \log((100)/(14))` and the value is w = 1.71

How to solve the equation for w

From the question, we have the following parameters that can be used in our computation:

`14 * 10^(0.5w) = 100`

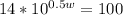
Divide both side by 14

So, we have

`10^(0.5w) = (100)/(14)`

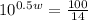
Take the logarithm of both sides

`\log(10^(0.5w)) = \log((100)/(14))`

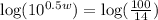
So, we have

`0.5w\log(10) = \log((100)/(14))`

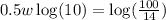
The log of base 10 is 1

So, we have

`0.5w = \log((100)/(14))`

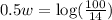
Divide both sides by 0.5

`w =2 \log((100)/(14))`

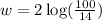
When the expression is evaluated, we have

w = 1.71

hence, the expression is
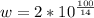`w = 2 * 10^{(100)/(14)}` and the value is w = 1.71

Answer 2

Given;

`14\cdot10^(0.5w)=100`

Divide both sides by 14, we have;

`\begin{gathered} (14\cdot10^(0.5w))/(14)=(100)/(14) \\ \\ 10^(0.5w)=(50)/(7) \end{gathered}`

Take the logarithm of both sides; we have;

`\log_(10)(10)^(0.5w)=\log_(10)((50)/(7))`

Applying logarithmic laws;

`0.5w=\log_(10)((50)/(7))`

Divide both sides by 0.5;

(b)