Question

1. Let a and b be integers. Prove that if a|b, then a”|6" for all positive integers n.

Answer 1

- a and b are integers. a | b means that integer a can divide integer b with no remainders.

- Let the Quotient of the division be k, so we can say:

`\begin{gathered} a|b=k \\ \\ \text{ Put in an easier way, we have:} \\ (b)/(a)=k \\ \\ where, \\ k\text{ is an integer since }a\text{ directly divides b} \end{gathered}`

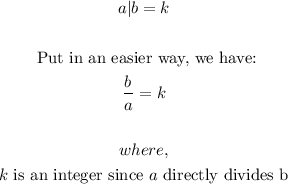
- Now, we are asked to find

`a^n|b^n`

- Again, we can rewrite this as:

`(b^n)/(a^n)`

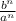
- We can rewrite this expression using the law of exponents that says:

`(x^m)/(y^m)=((x)/(y))^m`

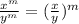
- Applying this law, we have:

`(b^n)/(a^n)=((b)/(a))^n`

- But we already know that

`(b)/(a)=k`

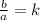
- Thus, we have that:

`\begin{gathered} (b^n)/(a^n)=k^n \\ \\ That\text{ is,} \\ a^n|b^n=k^n \\ for\text{ all positive integers n} \\ \\ k^n\text{ is an integer as well because }k\text{ is an integer.} \end{gathered}`

- Therefore, we have successfully proved the assertion