Question

PLEASE HELP

Given that LMR and SQP are
supplementary, m/RML = 20x + 14 and m/SQP = 14x - 4, find m/PQS

Answer 1

66°

Explanation:

Given:

• m∠LMR and m∠SQP are supplementary.
• m∠LMR = 20x + 14
• m∠SQP= 14x - 4

To find:

• m∠PQS

Solution:

We know that supplementary angles sum to 180 degrees, so we can write the following equation:

m∠LMR + m∠SQP = 180°

Substituting these expressions into the first equation, we get:

(20x + 14) + (14x - 4) = 180°

Combining like terms, we get:

34x + 10 = 180°

Subtracting 10 from both sides, we get:

34x = 170°

Dividing both sides by 34, we get:

`\sf x = (170^\circ)/(34)`

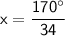
x = 5

We are also given that m∠PQS = m∠SQP(same angle), so we can find m∠PQS as follows:

m∠PQS = 14x - 4

Substituting x = 5, we get:

m∠PQS = 14(5) - 4

m∠PQS = 70 - 4

m∠PQS = 66°

Therefore, the measure of angle PQS is 66°

Answer 2

∠ PQS = 66°

Explanation:

supplementary angles sum to 180° , that is

∠ LMR + ∠ SQP = 180°

sum the 2 angles, equate to 180 and solve for x

20x + 14 + 14x - 4 = 180 ( collect like terms on left side )

34x + 10 = 180 ( subtract 10 from both sides )

34x = 170 ( divide both sides by 34 )

x = 5

Note that ∠ PQS = ∠ SQP ( reverse order of lettering , but same angle )

∠ PQS = 14x - 4 = 14(5) - 4 = 70 - 4 = 66°