Question

A student graphed the polynomial function P(x) = 2x3 − 9x2 + 12x − 4 on a computer, as shown below.

Part A: Use the graph to identify the zeros of the polynomial.
Part B: Describe the end behavior of the graph.

Answer 1

Part A

The roots or zeros of the polynomial are: 0.5 and 2

This is where the curve crosses or touches the x axis. The root x = 2 is easy to spot. The other root x = 0.5 isn't entirely obvious. I would use a graphing tool like GeoGebra or Desmos to determine the x = 0.5 root. If your teacher won't allow that, then another alternative is to use polynomial long division.

--------------------------------------------------------------

Part B

The end behavior is "falls to the left, rises to the right".

That's the informal way to describe it.

Translating "falls to the left" to notation leads to
`\text{As x} \to -\infty, \ \text{y} \to -\infty`

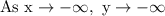
The "rises to the right" translates to the notation
`\text{As x} \to \infty, \ \text{y} \to \infty`