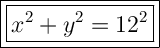Question

A circle has its center at the origin and has a diameter of 24 units.

What is the standard equation of the circle?
2
x² - y² = 24²
Ox² - y² = 12²
Ox² + y² = 12²
x² + y² = 24²

Answer 1

The standard equation of a circle with its center at the origin and a diameter of 24 units is x² + y² = 24².

Answer 2

`\textsf{C)} \quad x^2+y^2=12^2`

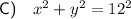
Explanation:

The standard equation of a circle with center (h, k) and radius (r) is:

`(x - h)^2 + (y - k)^2 = r^2`

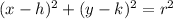
Given that the center of the circle is the origin (0, 0):

• 
  `h = 0`
• 
  `k = 0`

Therefore, the standard equation of a circle where its center is at the origin is:

`x^2 +y^2 = r^2`

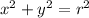
The radius of a circle is half its diameter.

Given the diameter of the circle is 24 units, then its radius is:

• r = 12

So, the standard equation of a circle that has its center at the origin and a diameter of 24 units is:

`\Large\boxed{\boxed{x^2+y^2=12^2}}`