Question

X^2-1<0 solve the inequality and interval notation

Answer 1

Solution: x = ± 1

Internal notation: (-1,1)

Explanation:

To solve the inequality x² - 1 < 0 , we can add 1 to both sides to get:

x² < 1

Then, we can take the square root of both sides to get:

`\sf x^2 < √(1)`

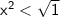
|x| < 1

This means that x must be between -1 and 1, but not equal to either -1 or 1.

In interval notation, this can be written as:

(-1, 1)

Therefore, the solution to inequality is: ± 1, and interval notation is (-1,1).