Given :
Rochelle is competing in a marathon.
She knows that once she runs 14.7 km she will have completed 35% of the marathon.
To Find :
Total length of the marathon.
Solution :
Let, total distance of the marathon is x km.
So, 35% of x is 14.7 .
In mathematics :
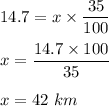
Therefore, total length of the marathon is 42 km.