Question

What kind of transformation converts the graph of f(x) = -10(x + 2)² + 1 into the graph of

g(x) = -10(x + 10)² + 1?
translation 8 units up
translation 8 units down
translation 8 units left
translation 8 units right
6

Answer 1

translation 8 units left

Explanation:

The transformation that converts the graph of f(x) = -10(x + 2)² + 1 into the graph of g(x) = -10(x + 10)² + 1 is atranslation 8 units to the left.

To see this, we can rewrite the graph of f(x) as follows:

`\sf f(x) = -10(x + 2)^2 + 1 = -10((x + 2)^2 - 1)`

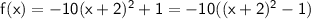
The graph of $g(x)$ can be rewritten as follows:

`\sf g(x) = -10(x + 10)^2 + 1 = -10((x + 2 + 8)^2 - 1)`

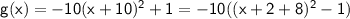
The only difference between the two equations is that the graph of g(x) has been translated 8 units to the left. This is because the term (x + 2 + 8) is 8 units more than the term (x + 2).

Here is a graph of the two functions to illustrate the transformation:

See Attachment:

As we can see, the graph of g(x) is simply the graph of f(x) shifted 8 units to the left.

Therefore, the answer is translation 8 units left.