Question

Solve the following problem using the substitution method

3x+3y=9
y=-5x-17

i just dont understand how to make the equation on the bottom look like a normal substitution equation. kinda like this ----------

--> (EX) 3x+y=5
5x-4y=-3


thank you for any help you can provide! ​

Answer 1

x = -5

y = 8

Explanation:

Given system of equations:

`\begin{cases}3x+3y=9\\y=-5x-17\end{cases}`

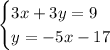
The substitution method is a technique used in algebra to solve a system of equations by isolating one variable in terms of the other from one equation and then substituting that expression into the other equation.

In the given system of equations, y has already been isolated in the second equation. Therefore, substitute this in place of y in the first equation to create an equation in terms of x only:

`3x+3(-5x-17)=9`

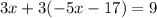
Distribute the 3:

`3x+3\cdot (-5x)+3\cdot (-17)=9`

`3x-15x-51=9`

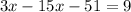
Combine like terms:

`-12x-51=9`

Add 51 to both sides of the equation:

`-12x-51+51=9+51`

`-12x=60`

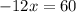
Divide both sides by -12:

`(-12x)/(-12)=(60)/(-12)`

`x=-5`

Therefore, the value of x is -5.

To find the value of y, simply substitute x = -5 into the second equation:

`y=-5(-5)-17`

`y=25-17`

`y=8`

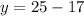
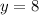
Therefore the solution to the given system of equations is:

• x = -5
• y = 8