Question

A line with a slope of – 6 passes through the points ( – 5,d) and ( – 4, – 5). What is the value of d?

Answer 1

d = 1

Explanation:

To find the value of d, we can use the formula for the slope of a line that passes through two points on the line.

The slope formula is:

`\boxed{m=(y_2-y_1)/(x_2-x_1)}`

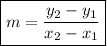
where (x₁, y₁) and (x₂, y₂) are the coordinates of two points on the line.

In this case:

• m = -6
• (x₁, y₁) = (-5, d)
• (x₂, y₂) = (-4, -5)

Substitute the given values into the slope formula:

`-6=(-5-d)/(-4-(-5))`

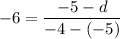
Simplify the equation:

`-6=(-5-d)/(-4+5)`

`-6=(-5-d)/(1)`

`-6=-5-d`

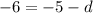
Add d to both sides of the equation:

`-6+d=-5-d+d`

`d-6=-5`

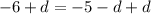
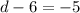
Finally, add 6 to both sides of the equation:

`d-6+6=-5+6`

`d=1`

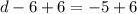
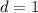
Therefore, the value of d is 1.

`\Large\boxed{\boxed{d=1}}`