Question

If f is defined by the function f(x)=x-4/x-2 then lim f(x) is equivalent to which of the following

Answer 1

The correct answer is the third option:

`\lim_(x\to4)(√(x)-2)`

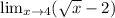
Step-by-step explanation:

We have the function:

`f(x)=(x-4)/(√(x)-2)`

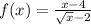
In the numerator, we have x - 4. We can rewrite it as a difference of squares, since:

`\begin{gathered} x=(√(x))^2 \\ 4=2^2 \end{gathered}`

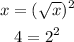
Thus:

`x-4=(√(x)-2)(√(x)+2)`

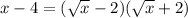
Then, the limit:

`\begin{gathered} \lim_(x\to4)(((√(x)-2)(√(x)+2))/((√(x)-2)) \\ \end{gathered}`

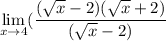
We can cancel out the terms, since we are taking limit, this is, numbers that infinitely close to 4, bt never 4. This way we can cancel the terms, and get:

`\lim_(x\to4)(√(x)+2)`