Answer:
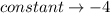
Step-by-step explanation: We have to find the constant that when multiplied to the first equation and added to the second, the variable x gets canceled out, the two equations are as follows:

Multiplying the equation (1) by -4 and adding it to the equation (2) gives the following answer:
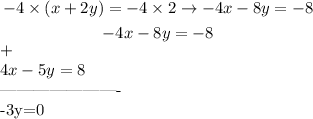
Therefore the value of the constant is -4.