Question

Find the absolute extrema of the function (if any exist) on each interval. (If an answer does not exist, enter DNE.)

Answer 1

To find the absolute extrema of a function on an interval, analyze the endpoints and critical points. The absolute extrema are the maximum and minimum values of the function.

Step-by-step explanation:

To find the absolute extrema of a function, we need to analyze the endpoints of the interval and any critical points within the interval. The critical points occur where the derivative of the function equals zero or is undefined. The absolute extrema will be the maximum and minimum values of the function on the given interval.

For example, let's say we have the function f(x) = x^2 on the interval [0,5]. We first calculate the derivative f'(x) = 2x. We find that the derivative is zero at x = 0. This critical point needs to be checked as it could be a maximum or minimum. Plugging in the endpoints of the interval, we get f(0) = 0^2 = 0 and f(5) = 5^2 = 25. Comparing these values, we see that the absolute minimum is 0 at x = 0 and the absolute maximum is 25 at x = 5.

Answer 2

Before we can determine the absolute extrema of the function, let's graph the given function first. f(x) = x² - 6x.

For the interval [-1, 6], we can see that the maximum value would be at x = -1.

Let's replace x with -1 in the function above.

`\begin{gathered} f(x)=x^2-6x \\ f(-1)=(-1)^2-6(-1) \\ f(-1)=1+6 \\ f(-1)=7 \end{gathered}`

Therefore, the maximum between the interval [-1, 6] is at (-1, 7).

On the other hand, looking at the interval (3, 7] in the graph, the maximum is found at x = 7. To determine the maximum point, replace "x" with 7 in the function above.

`\begin{gathered} f(7)=7^2-6(7) \\ f(7)=49-42 \\ f(7)=7 \end{gathered}`

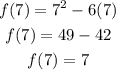
Therefore, the maximum at the interval (3, 7] is at point (7, 7).