Hi there! I'll help you solve this problem!
In order for two lines to be parallel, their slopes should be equal.
We have two lines:
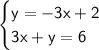
Let's convert the second equation to slope-intercept (y = mx + b) form.
To do it, move 3x to the other side, using the opposite operation:
Now the lines are:
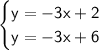
Both lines have a slope of -3. which means their slope is the same.
Therefore, they are parallel.
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
Best wishes!