Question

I inserted a picture of the questionif it helps i can give you my answer to my previous question

Answer 1

In order to determine the time it takes for the music player to fall to the bottom of the ravine, we shall find the solutions of t as follows;

`\begin{gathered} t=\sqrt[]{(8t+24)/(16)} \\ \end{gathered}`

Take the square root of both sides;

`\begin{gathered} t^2=(8t+24)/(16) \\ \text{Cross multiply and we'll have;} \\ 16t^2=8t+24 \\ \text{ Re-arrange the terms and we'll now have;} \\ 16t^2-8t-24=0 \end{gathered}`

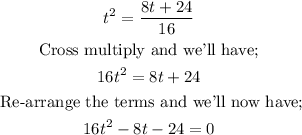
We can now solve this using the quadratic equation formula;

`\begin{gathered} \text{The variables are;} \\ a=16,b=-8,c=-24 \\ t=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ t=\frac{-(-8)\pm\sqrt[]{(-8)^2-4(16)(-24)_{}}}{2(16)} \\ t=\frac{8\pm\sqrt[]{64+1536}}{32} \\ t=\frac{8\pm\sqrt[]{1600}}{32} \\ t=(8\pm40)/(32) \\ t=(8+40)/(32),t=(8-40)/(32) \\ t=(48)/(32),t=-(32)/(32) \\ t=1.5,t=-1 \end{gathered}`

We shall now plug each root back into the original equation, as follows;

`\begin{gathered} \text{Solution 1:} \\ \text{When t}=1.5 \\ t=\sqrt[]{(8t+24)/(16)} \\ t=\sqrt[]{(8(1.5)+24)/(16)} \\ t=\sqrt[]{(12+24)/(16)} \\ t=\sqrt[]{(36)/(16)} \\ t=(6)/(4) \\ t=1.5\sec \end{gathered}`
`\begin{gathered} \text{Solution 2:} \\ \text{When t}=-1 \\ t=\sqrt[]{(8(-1)+24)/(16)} \\ t=\sqrt[]{(-8+24)/(16)} \\ t=\sqrt[]{(16)/(16)} \\ t=(4)/(4) \\ t=1 \end{gathered}`

From the result shown the ballon will deploy after 1.5 seconds for the first solution.

However t = -1 cannot be a solution since you cannot have a negative time (-1 sec)

ANSWER:

t =1.5 is a solution