Question

Find the m < WQZ

please show steps

Answer 1

128 degrees

Explanation:

<WQZ and <XQZ are supplementary angles, as they are on the same line and split by a line. Thus, their angles add up to 180 degrees. That gives us the equation:

180 = <WQZ + <XQZ

180 = (9x+2) + (3x+10)

180 = 9x + 3x + 2 + 10

180 = 12x + 12

Subtract 12 from both sides:

168 = 12x

Divide both sides by 12:

14 = x

x = 14

Plus that back into the original equation for <WQZ:

<WQZ = 9x+2

<WQZ = 9(14) + 2

<WQZ = 126 + 2

<WQZ = 128

Thus, we get our final answer that <WQZ is 128 degrees.

Answer 2

m ∠WQZ = 128°

Explanation:

A linear pair is a pair of adjacent angles that form a straight line. In other words, the sum of the measures of the two angles in a linear pair is always 180 degrees.

In this case:

m ∠WQZ and m∠ XQZ are angles of linear pair.

So,

m ∠WQZ + m∠ XQZ = 180°

Substitute the given value:

(9x+2)° +(3x + 10)° = 180°

9x + 2 + 3x + 10 = 180

Simplify like terms:

12x + 12 = 180

Subtract 12 on both sides:

12x + 12 - 12 = 180 - 12

12x = 168

Divide both sides by 12.

`\sf (12x)/(12) =( 168)/(12)`

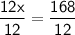
x = 14

Now, we can find the value of angle m ∠WQZ by substituting the value of x.

m ∠WQZ = (9x+ 2)° = (9×14+2)° = (126+2)° = 128°

Therefore,

m ∠WQZ = 128°