Question

What is the distance between points Enter the answer in the box. units (11, 3) and (4, 3). on a coordinate plane?​

Answer 1

Step-by-step explanation: The distance between points (11, 3) and (4, 3) on a coordinate plane is 7 units. To calculate the distance between two points on a coordinate plane, we can use the distance formula:
`d = \sqrt{(X_(2) - X\\_(1) )^(2) + (y_(2) - y_(1)^(2) ) } }`

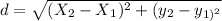
where (x1, y1) and (x2, y2) are the coordinates of the two points, In this case we have:
`d = \sqrt{(4-11)^(2) + (3-3)^(2) = \sqrt{(-7)^(2) + 0^2} } =√(49) = 7`

Therefore, the distance between points (11, 3) and (4, 3) is 7 units.

Hopes this helps!

Answer 2

d = 7

Explanation:

Start by using the distance formula.

d=
`\sqrt{ (x_(2) - x_(1) )^2 + (y_(2) - y_(1))^2`

let's use (4,3) as (x1,y1) and (11,3) as (x2, y2)

so,

d =
`√((11-4)^2 + (3-3)^2)`

d =
`√((7)^2 + (0)^2)`

d =
`√((7)^2)`

d =
`√(49)`

d = 7