Question

Through (3,13), parallel to 3x+5y=29

Answer 1

Hi there! I'll help you solve this problem!

We are asked to find the equation of a line, given that:

• The line is parallel to 3x + 5y = 29
• The line passes through the point (3,13)

step one

So first, let's convert 3x + 5y = 29 to slope-intercept form.

Slope-intercept form

• Slope intercept is a way of writing the equation of a line. It's formatted as
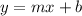  `y=mx+b` where the parameter
  `m` defines the slope and
  `b` defines the y-intercept.

Basically, we need to convert the equation
`3x+5y=29`, which is in standard form, to
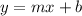`y=mx+b`, which is slope intercept form.

So first, we subtract 3x from both sides:

`5y=29-3x`

Next, divide both sides by 5

`y=\cfrac{29-3x}{5}`

Rewrite it this way:

`y=\cfrac{29}{5}-\cfrac{3x}{5}`

Our equation is now in slope intercept form. The next step is to figure out the values of m and b.

• m = -3/5
• b = 29/5

step two

But that's the slope of the "old" line - what about the slope of the new line? Well, that we'll determine soon. Remember that the new line is parallel to y = 29/5 - 3x/5. Well, guess what? Parallel lines actually have the same slope! So the new line has the same slope as the line

y = 29/5 - 3x/5, which is -3/5.

step three

Now that we know the slope and the point that the line intersects, we can get down to writing our equation in point-slope form.

Point-slope form is
`\boldsymbol{y-y_1=m(x-x_1)}`.

Substitute the values:

• 
  `\boldsymbol{y-13=-\cfrac{3}{5}(x-3)}}`

Now we need to simplify that, and convert that to slope-intercept form!

step four

Distribute -3/5:

`\boldsymbol{y-13=-\cfrac{3}{5}x-\cfrac{3}{1}*-\cfrac{3}{5}}`

Simplify:

`\boldsymbol{y-13=-\cfrac{3}{5}x+\cfrac{3*3}{5}}`

`\boldsymbol{y-13=-\cfrac{3}{5}x+\cfrac{9}{5}}`

The next step is to add 13 to both sides:

`\boldsymbol{y=-\cfrac{3}{5}x-\cfrac{9}{5}+\cfrac{13}{1}}`

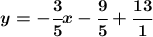
Uh oh! These fractions have different denominators - we can't add them just now! So, we need to write a common denominator:

`\boldsymbol{y=-\cfrac{3}{5}x+\cfrac{9}{5}+\cfrac{13\cdot5}{5}}`

`\boldsymbol{y=-\cfrac{3}{5}x+\cfrac{9}{5}+\cfrac{65}{5}}`

`\boldsymbol{y=-\cfrac{3}{5}x+\cfrac{65+9}{5}}`

`\boxed{\boxed{\boldsymbol{y=-\cfrac{3}{5}x+\cfrac{74}{5}}}}`

Therefore, the equation of the line that passes through the point (3,13) and is parallel to 3x + 5y = 29 is y = -3/5x + 74/5.

<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<

Best wishes!

Answer 2

3x + 5y = 74

Explanation:

To find the equation of a line that passes through the point (3,13) and is parallel to the line 3x + 5y = 29, we can use the fact that two parallel lines have the same slope. The given line has the equation 3x + 5y = 29. We need to find the slope of this line, and then we can use it to write the equation of the parallel line.

First, let's rearrange the equation 3x + 5y = 29 to solve for y:

3x + 5y = 29

Subtract 3x from both sides:

3x + 5y - 3x = 29 - 3x

5y = -3x + 29

Now, divide both sides by 5 to isolate y:

`\sf (5y)/(5)=-(3)/(5)x+(29)/(5)`

`\sf y=-(3)/(5)x+(29)/(5)`

While comparing with y = mx + c, we get

`\sf m =-(3)/(5)`

So, the slope of the given line is
`\sf -(3)/(5)`.

Now that we know the slope, we can use the point-slope form of a line to write the equation of the parallel line:

`\sf y - y_1 = m(x - x_1)`

Where (x1, y1) is the point (3,13) and m is the slope, which is -3/5.

Now, substitute the given value:

`\sf y - 13 = -(3)/(5)(x - 3)`

Now, distribute the slope and simplify:

`\sf y - 13 = -(3)/(5)x + (9)/(5)`

y - 13 = (-3/5)x + 9/5

To get rid of the fraction, we can multiply both sides of the equation by 5:

`\sf 5(y - 13) = -3x + 9`

Now, distribute the 5 on the left side:

`\sf 5y - 65 = -3x + 9`

Add 65 to both sides to isolate -3x:

`\sf 5y - 65+65 = -3x + 9 + 65`

`5y = -3x + 74`

Now, we can rewrite the equation in the standard form (Ax + By = C):

3x + 5y = 74

So, the equation of the line that passes through (3,13) and is parallel to 3x + 5y = 29 is 3x + 5y = 74.