Yes, there is a triangle with angles measuring 90 degrees, 90 degrees, and 45 degrees.
Clue 1: Definition of Right Isosceles Triangle
Start by understanding what a right isosceles triangle is. It's a triangle with two equal angles of 45 degrees and one right angle of 90 degrees.
Clue 2: Identify the Angles and Sides
Recognize the unique angles and side lengths in a right isosceles triangle: 45 degrees, 45 degrees, and 90 degrees, as well as the two equal sides (legs) and one longer side (hypotenuse).
Clue 3: Knowledge of the Pythagorean Theorem
Remember the Pythagorean theorem, which relates the sides of a right triangle:
 where 'c' is the hypotenuse, and 'a' and 'b' are the legs.
where 'c' is the hypotenuse, and 'a' and 'b' are the legs.
Clue 4: Special Right Triangle Relationships
Know that right isosceles triangles are a type of special right triangle, along with 30-60-90 triangles, and they have specific relationships between angles and side lengths.
Clue 5: Applications in Construction
Consider real-world applications of right isosceles triangles, such as their use in ensuring accurate right angles in construction and engineering.
Clue 6: Role in Trigonometry
Understand that right isosceles triangles are fundamental in trigonometry, where they help define trigonometric functions like sine, cosine, and tangent.
Clue 7: Geometric Construction
Appreciate that you can construct right isosceles triangles using compass and straightedge techniques, which is a valuable geometric skill.
Clue 8: Connection to Other Types of Triangles
Recognize the relationships between right isosceles triangles, equilateral triangles, and other types of isosceles triangles.
Clue 9: Real-World Examples
Look for real-world examples where right isosceles triangles are used, such as in road signs and highway markers.
Clue 10: Putting it All Together
Finally, combine your knowledge of right isosceles triangle properties, the Pythagorean theorem, and their real-world applications to arrive at a well-rounded answer when discussing them.
Paragraph 1: Introduction to Right Isosceles Triangles
A right isosceles triangle is a specific type of triangle with two equal angles of 45 degrees and a right angle of 90 degrees. In this discussion, we will explore the properties and characteristics of these unique triangles.
Paragraph 2: Definition and Properties
A right isosceles triangle is defined by its two equal sides, known as the legs, and one right angle. The angles opposite the legs are congruent, each measuring 45 degrees. The hypotenuse, opposite the right angle, is longer and is determined by the Pythagorean theorem.
Paragraph 3: The Pythagorean Theorem
The Pythagorean theorem is a fundamental mathematical principle that relates the lengths of the sides of a right triangle. In a right isosceles triangle, it can be used to find the length of the hypotenuse, c, when the lengths of the legs, a and b, are known:
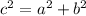
Paragraph 4: Special Right Triangle Relationship
A right isosceles triangle is a type of special right triangle, alongside the 30-60-90 triangle. These triangles have unique relationships between their side lengths and angles, making them useful in various mathematical and geometric applications.
Paragraph 5: Use in Construction
Right isosceles triangles are commonly used in construction and engineering. For example, when constructing 90-degree corners, such as in buildings, the presence of right isosceles triangles ensures accuracy.
Paragraph 6: Application in Trigonometry
The study of right isosceles triangles is essential in trigonometry, where they serve as the foundation for understanding trigonometric functions, such as sine, cosine, and tangent. These functions are crucial for solving problems involving angles and distances.
Paragraph 7: Geometric Construction
Right isosceles triangles can be constructed using compass and straightedge techniques. This is a fundamental skill in geometry and provides a hands-on way to explore the properties of these triangles.
Paragraph 8: Relationship to Other Types of Triangles
Right isosceles triangles have a connection to other types of triangles, such as equilateral and isosceles triangles. An equilateral triangle is a special case of an isosceles triangle, and the right isosceles triangle can be used as a basis for understanding these relationships.
Paragraph 9: Real-World Examples
Right isosceles triangles can be found in everyday life. For instance, in road signs, the reflective markers on highways form a pattern of right isosceles triangles, ensuring visibility and safety for drivers.
Paragraph 10: Conclusion
In conclusion, right isosceles triangles are fascinating geometric shapes with unique properties and applications in mathematics, engineering, and everyday life. Understanding their properties and relationships to other triangles is valuable in various fields and provides insights into the world of geometry and trigonometry.