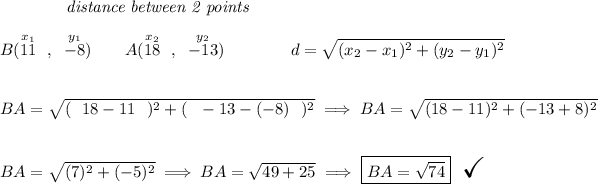Question

Prove that the point A (18,-13) lies on the circle centered at B(11,-8) that passes through the point C(4,-3). What is the RADIUS of the circle?

Answer 1

well, we know the circle has a center at B(11 , -8) and it passes through C(4 , -3), so the distance from B to C is really just its radius. Now, if it's true that point A(18 , -13) is really on that circle, then the distance from B to A must also be the same as from B to C, since it's the radius and all points of the circle are equidistant from the center. Let's check

`~~~~~~~~~~~~\textit{distance between 2 points} \\\\ B(\stackrel{x_1}{11}~,~\stackrel{y_1}{-8})\qquad C(\stackrel{x_2}{4}~,~\stackrel{y_2}{-3})\qquad \qquad d = √(( x_2- x_1)^2 + ( y_2- y_1)^2) \\\\\\ BC=√((~~4 - 11~~)^2 + (~~-3 - (-8)~~)^2)\implies BC=√((4 -11)^2 + (-3 +8)^2) \\\\\\ BC=√( (-7)^2 + (5)^2) \implies BC=√( 49 + 25)\implies \boxed{BC=√( 74 )} \\\\[-0.35em] ~\dotfill`

`~~~~~~~~~~~~\textit{distance between 2 points} \\\\ B(\stackrel{x_1}{11}~,~\stackrel{y_1}{-8})\qquad A(\stackrel{x_2}{18}~,~\stackrel{y_2}{-13})\qquad \qquad d = √(( x_2- x_1)^2 + ( y_2- y_1)^2) \\\\\\ BA=√((~~18 - 11~~)^2 + (~~-13 - (-8)~~)^2)\implies BA=√((18 -11)^2 + (-13 +8)^2) \\\\\\ BA=√( (7)^2 + (-5)^2) \implies BA=√( 49 + 25)\implies \boxed{BA=√( 74 )} ~~ \textit{\LARGE \checkmark}`