Question

What is an equation of the line that passes through the point (6, —1) and is parallel to the line 3x + 2y = 2?

Answer 1

3x +2y = 16

Explanation:

linear equation in standard form:

Given line: 3x + 2y = 2

Parallel lines have same slope. Find the slope using the equation of the given line. Let us write the equation in slope intercept form.

3x + 2y = 2

2y = -3x + 2

`\sf y = (-3)/(2)x + (2)/(2)\\\\\\y = (-3)/(2)x + 1`

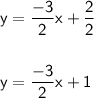
Comparing with y = mx + b, slope = (-3/2)

Slope = -3/2

Equation of the required line:

`\sf y = (-3)/(2)x + b`

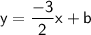
This line is passing through (6 ,-1). Substitute the x and y in the above equation and find the y-intercept.

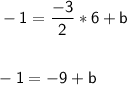
`\sf -1 = (-3)/(2)*6 + b\\\\\\-1 = -9 + b\\\\`

-1 + 9 = b

b = 8

`\sf y = (-3)/(2)x + 8\\\\\text{Multiply the entire equation by 2}\\\\2y = 2*(-3)/(2)x+2*8\\\\2y = -3x + 16\\\\\boxed{\bf 3x + 2y = 16}`

Answer: Equation of the line in standard form:

3x + 2y = 16