Question

Question 1.

5x+2y=-7
15x+6y=21
No solution, One solution, or infinite solution?

Question 2.
Y=2x+1
2x-4=1
No solution, one solution, or infinite solution?

Question 3.
6x+4y=10
3x+2y=5
No solution, one solution, or infinite solution?

Answer 1

Question 1

Answer: No solution

-------------------

Step-by-step explanation:

Multiply both sides of the first equation by 3. Doing so leads to

3*(5x+2y) = 3*(-7)

15x+6y = -21

The second equation is 15x+6y = 21

Let's say we let z = 15x+6y

This means the system

`\begin{cases}15x+6y = -21\\15x+6y = 21\end{cases}`

becomes

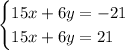
`\begin{cases}z = -21\\z = 21\end{cases}`

but we can't have z be equal to more than one value at a time. We have a contradiction and therefore there are no solutions.

===============================================

Question 2

Answer: One solution

The solution is (x,y) = (5/6)

-------------------

Step-by-step explanation:

Apply substitution

2x - 4y = 1

2x - 4(2x+1) = 1

2x - 8x - 4 = 1

-6x - 4 = 1

6x = 1+4

6x = 5

x = 5/6

Then use this to find y

y = 2x+1

y = 2(5/6)+1

y = 5/3 + 1

y = 5/3 + 3/3

y = 8/3

The one solution is (x,y) = (5/6)

===============================================

Question 3

Answer: Infinitely many solutions

-------------------

Step-by-step explanation:

Multiply both sides of the second equation by 2

3x+2y = 5 becomes 2*(3x+2y) = 2*5 which turns into 6x+4y = 10

This is exactly identical to the first equation of the original system given.

So both equations represent the same thing. We have infinitely many intersection points, and infinitely many solutions.

All of these solutions are on the line 3x+2y = 5

Answer 2

Q1: no solution

Q2: one solution

Q3: infinite solutions

Step-by-step explanation: