Question

What is the equation in slope-intercept form of the of the line that goes through the point (15,-3)and (6,-12)

Answer 1

y = 1x - 18

Explanation:

To find the equation of the line in slope-intercept form that goes through the points (15, -3) and (6, -12), we can use the following steps:

Step 1: Calculate the slope of the line.

The slope of a line is calculated using the following formula:

`\sf m = (y_2 - y_1)/(x_2 - x_1)`

where (x1, y1) and (x2, y2) are two points on the line.

In this case, we have:

`\sf m = ( - 12 -(-3))/(6-15)= (-9)/(-9)=1`

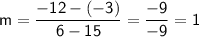
Step 2: Use the slope and one of the points to find the y-intercept of the line.

We can use the following formula to find the y-intercept of the line:

b = y - mx

where (x, y) is a point on the line and m is the slope of the line.

In this case, we can use the point (15, -3) to find the y-intercept.

b = -3 - 1(15)

b = -18

Step 3: Write the equation of the line in slope-intercept form by substitution of known value:

The equation of a line in slope-intercept form is:

y = mx + b

where m is the slope of the line and b is the y-intercept.

In this case, the equation of the line is:

y = 1x - 18

Therefore, the equation of the line in slope-intercept form that goes through the points (15, -3) and (6, -12) is y = x - 18.