Question

a cross was performed in c. elegans, following the segregation of three linked genes, where the genetic map was a-----16cm-----b----9cm----c. the cross was performed between a parent with genotype abc/abc and a parent with genotype abc/abc. the f1 progeny were then testcrossed. assuming an interference value of 24%, what proportion of the progeny is expected to be abc/abc?

Answer 1

The question deals with the expected proportions of a specific genotype in the progeny from a testcross of C. elegans with linked genes, taking into account the recombination frequencies and an interference value that affects the likelihood of crossovers.

Step-by-step explanation:

The student is asking about the expected proportion of progeny with a specific genotype (abc/abc) from a testcross involving C. elegans with three linked genes on a chromosome. The alleles for these genes are separated by genetic distances of 16 centimorgans (cM) and 9 cM. With an interference value of 24%, we calculate the expected proportions using the genetic map and recombination frequencies. The interference affects the likelihood of crossovers in linked genes, thus altering the expected proportions.

Calculating the exact proportion of abc/abc progeny requires knowledge of the recombination frequencies and how interference adjusts these frequencies. Typically, with no interference, the expected progeny can be calculated using a forked-line diagram or a Punnett square to assess independent assortment probabilities. However, when genes are linked and interference is present, the calculation becomes more complex. Recombination frequencies need to be adjusted according to the interference value to predict the expected proportions of offspring accurately.

Answer 2

The proportion of progeny expected to be
`\( \text{abc/abc} \)` in the testcross of
`\( \text{C. elegans} \)`, considering the given recombination frequencies and an interference value of 24%, is approximately 76.09%.

To determine the proportion of
`\( \text{abc/abc} \) progeny in a testcross involving linked genes in \( \text{C. elegans} \),` we need to consider genetic linkage, recombination frequencies, and the concept of interference. Let's break it down step by step:

1. Understanding the Cross:

- The initial cross is between two homozygous individuals with the genotype
`\( \text{abc/abc} \). Their F1 progeny will all be heterozygous \( \text{abc/abc} \).`

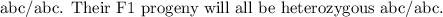
- A testcross involves crossing these F1 progeny with a homozygous recessive individual. However, since the problem doesn't specify the recessive alleles, we'll assume it's the same genotype

2. Genetic Map

- The map distance between genes a and b is 16 cM (centiMorgans), and between b and c is 9 cM.

3. Recombination Frequency:

- The recombination frequency between genes is approximately equal to the map distance (in cM) divided by 100. Therefore, the recombination frequency between a and b is 16%, and between b and c is 9%.

4. Interference and Coincidence:

- Interference is the phenomenon where a crossover in one region of a chromosome inhibits crossovers in an adjacent region. It's calculated as
`\( 1 - \text{coincidence} \),` where coincidence is the observed double crossover rate divided by the expected double crossover rate.

- Here, we have an interference of 24%, meaning the actual double crossover events are reduced by this amount.

5. Calculating Expected Double Crossovers:

- The expected double crossover frequency (without interference) between a and c is the product of the individual frequencies:
`\(0.16 * 0.09 = 0.0144 \)` or 1.44%.

- With 24% interference, the actual double crossover frequency is

6. Proportion of abc/abc Progeny:

- The progeny with the
`\( \text{abc/abc} \)`genotype result from either no crossover events or double crossovers between a and c .

- The probability of no crossovers is simply the complement of any crossovers occurring, which is
`\( 1 - (0.16 + 0.09 - \text{double crossover frequency}) \).`

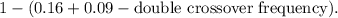
Let's calculate the exact proportion of
`\( \text{abc/abc} \)` progeny expected:

The proportion of progeny expected to be
`\( \text{abc/abc} \)` in the testcross of
`\( \text{C. elegans} \)`, considering the given recombination frequencies and an interference value of 24%, is approximately 76.09%. This accounts for both scenarios where no crossover events occur and scenarios involving double crossovers between genes a and c .