Answer:
The solution of the system of equation is (3,8)
Explanation:
We are given that
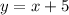 ...(1)
...(1)
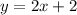 ...(2)
...(2)
We have to graph the system of linear equation.
For equation (1)
Substitute x=0
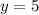
Substitute y=0

Therefore, we obtained two points (0,5) and (-5,0) for equation (1).
For equation (2)
Substitute x=0
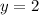
Substitute y=0
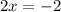
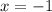
Therefore, we obtained two points (0,2) and (-1,0) for equation (2).
Now, we find intersection point of two equation
Substract equation (2) from (1)
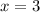
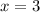
Substitute x=3 in equation (1)
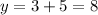
The intersection point of two equation is at (3,8).
Hence, the solution of given system of equation is (3,8).